Heterocedasticidad

Concepto

La palabra heterocedasticidad surge de la unión de dos palabras: “hetero” (diferente) y “cedasticidad” (dispersión), es decir, varianza diferente.

Causas de la heterocedasticidad

En el modelo de regresión lineal, (Y = Xβ+u), uno de los supuestos que se establece, para poder estimar el modelo por mínimos cuadrados ordinarios, y así obtener estimaciones eficientes de los parámetros, es que las perturbaciones del modelo tienen que ser homocedásticas, es decir, su varianza se mantiene constante para todas las observaciones de la muestra, E(u²) = σ². Sin embargo, si este supuesto deja de cumplirse entonces el termino de error tiene heterocedasticidad, E(u²) = σ²_i, i=1,...,N.

Entre los motivos que pueden hacer que la varianza de las perturbaciones no se mantenga constante podemos destacar los siguientes:

• a) Por ejemplo, si se plantea un modelo de gasto en función del nivel de renta, que pueden tener diferentes familias, empresas, países, etc. es muy posible que el nivel de gasto tenga una mayor dispersión en aquellos que tengan un nivel de renta mayor.
• b) Si para el modelo planteado, los datos con los que se trabaja son promedios de diferentes grupos, entonces, las varianzas son inversamente proporcionales al número de individuos de cada grupo.
• c) En los modelos de aprendizaje sobre errores, la heterocedasticidad puede surgir si a medida que transcurre el tiempo, y se aprende, la varianza de los errores cometidos es cada vez menor.
• d) La existencia de outliers o valores atípicos (valores excesivamente grandes o pequeños respecto del resto de valores de la muestra) sobre todo, en muestras pequeñas, hace que la inclusión o no de estos valores altere sustancialmente los resultados de la estimación.
• e) La existencia de asimetría en las variables explicativas del modelo hace que se produzca heterocedasticidad si existe, por ejemplo, una mayor concentración de recursos en unos entes que en otros.
• f) La mala especificación de un modelo, debida, por ejemplo, a la omisión de una variable relevante en el modelo, puede hacer que la varianza del término de error no se mantenga constante.
• g) Si los datos con los que se trabaja en el modelo no están correctamente transformados, por ejemplo no se toman las diferencias adecuadas o se trabaja con variables que no están en logaritmos cuando tienen que tener esta transformación, entonces también puede dar lugar a la existencia de heterocedasticidad.

La existencia de heterocedasticidad suele ser más común cuando se trabaja con datos de corte transversal que cuando se trabaja con datos de series temporales.

Consecuencias de la heterocedasticidad

Si las perturbaciones de un modelo de regresión lineal tienen heterocedasticidad, entonces el estimador de mínimos cuadrados ordinarios (MCO) sigue siendo lineal e insesgado, pero deja de ser eficiente, ya que no es el estimador de mínima varianza.

Por lo tanto, para estimar el modelo de forma correcta en presencia de heterocedasticidad no se puede utilizar el estimador MCO. El estimador correcto es el que obtiene utilizando mínimos cuadrados generalizados (MCG). El estimador MCG es lineal, insesgado y eficiente.

Formas de detectar la heterocedasticidad

Para detectar la heterocedasticidad, básicamente, se pueden utilizar dos métodos: uno informal, basado en la representación gráfica de los residuos frente alguna de las variables del modelo, y otro formal, que consiste en la realización de diferentes tipos de contrastes.

Método gráfico

Cuando no se tiene inicialmente ningún tipo de información sobre cuál puede ser la forma de la heterocedasticidad, lo que se suele hacer en la práctica es estimar primero el modelo bajo el supuesto de que no existe heterocedasticidad y, posteriormente, obtener los residuos y realizar un gráfico de los residuos al cuadrado frente a la variable estimada o frente a las variables explicativas del modelo. Así, si no existe ningún patrón sistemático entre las variables, entonces, posiblemente, no habrá heterocedasticidad en los datos y, por el contrario, si existe un patrón definido puede ayudar a determinar cuál es el tipo de heterocedasticidad.

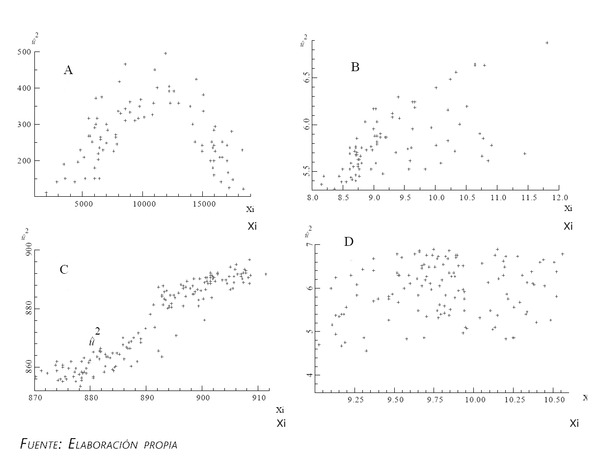
En el gráfico anterior, se puede apreciar que las figuras A, B y C muestran patrones definidos. Por ejemplo, la figura A indica una relación cuadrática entre el cuadrado de los residuos y la variable X; en la figura B se comprueba que la dispersión aumenta a medida que las variables toman valores mayores; y la figura C sugiere una relación lineal entre los residuos y la variable X_i. En la figura D no existe un patrón sistemático entre las dos variables.

Contrastes de heterocedasticidad

Existen diversos contrastes de heterocedasticidad. Cada uno de estos contrastes plantea como hipótesis nula la ausencia de heterocedasticidad pero se diferencian entre sí en la forma de plantear la hipótesis alternativa. Algunos plantean como hipótesis alternativa la forma funcional de la heterocedasticidad y otros no. Algunos de los contrastes de heterocedasticidad más utilizados se muestran a continuación:

— Contraste de Golfeld y Quandt (1965). Este contraste supone que la varianza de las perturbaciones está relacionada, normalmente, con alguna de las variables explicativas del modelo. Bajo el supuesto de que dicha dependencia sea, por ejemplo, positiva (los menores/mayores valores de la varianza se producen cuando los valores de la variable son menores/mayores), el contraste se desarrolla del siguiente modo:

• a) Se ordenan de menor a mayor los valores de la variable.
• b) Se omiten p observaciones centrales.
• c) Se estiman dos modelos: uno para las primeras 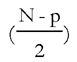observaciones y otro para las 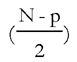últimas observaciones. Se obtienen las sumas residuales de las dos regresiones (SR1 y SR2).
• d) Bajo el supuesto de homocedasticidad y Normalidad del término de error entonces el cociente.

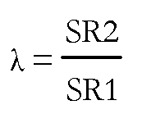
sigue una distribución F con un número de grado de libertad del numerador y denominador iguales a 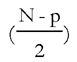-k. Donde N es el número total de datos y k el número de variables explicativas del modelo.

Ejemplo. Para datos trimestrales de consumo (Y) y renta (X) en el período comprendido entre 1969 y 2008. Eliminando las observaciones centrales se obtienen las siguientes estimaciones, donde los valores entre paréntesis son las desviaciones típicas estimadas.

Regresión para las primeras 60 observaciones:

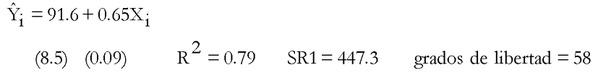
Regresión para las últimas 60 observaciones:

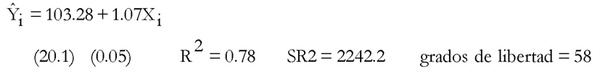
Con estos resultados se obtiene que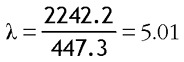

El valor crítico para la F con 58 grados de libertad para el numerador y 58 para el denominador, al nivel de significación del 5 % es, aproximadamente, 1.5. Como el valor estimado de λ es mayor que el valor crítico entonces se puede concluir diciendo que hay heterocedasticidad en la varianza del término de error.

Este contraste depende del número de datos que se omitan y de la identificación correcta de la variable que servirá como referencia para ordenar las variables y detectar la heterocedasticidad. Para solventar este problema se puede utilizar el siguiente contraste.

— Contraste de Breush-Pagan-Godfrey. En una regresión se supone que la varianza del término de error depende de un vector de p variables Z, del siguiente modo:

σ²_i= f(β₀ + β₁Z_1i + ... + β_pZ_pi)

Si todos los parámetros de la combinación lineal, excepto el término independiente son estadísticamente nulos, entonces no habría heterocedasticidad. Para realizar este contraste se realizan los siguientes pasos:

• a) Se estima el modelo de regresión lineal por mínimos cuadrados ordinarios y se obtienen los residuos.
• b) Se normalizan los residuos al cuadrado del siguiente modo: 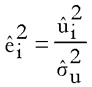, donde 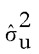es la estimación máximo verosímil de la varianza del término de error bajo el supuesto de homocedasticidad.
• c) Se estima una regresión de los residuos normalizados sobre una constante y las p variables explicativas.
• d) Obtener la suma explicada de la regresión (SE). Bajo la hipótesis nula de homocedasticidad y Normalidad del término de error, el cociente 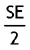sigue una distribución x²_p.

Ejemplo, con los mismos datos trimestrales del ejemplo anterior se obtiene el siguiente modelo estimado:

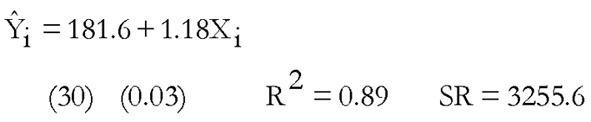
Se normalizan los residuos. Los resultados de la regresión de los residuos sobre una constante y la variable explicativa son:

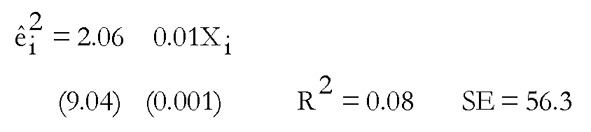
Entonces 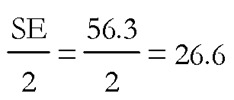y como el valor crítico de la χ²₁ es 3.84, se rechaza la hipótesis nula, lo que evidencia la existencia de heterocedasticidad.

— Contraste de White (1980). A diferencia de los contrastes anteriores este contraste no se basa en el supuesto de Normalidad y tampoco necesita especificar cual es la forma funcional de la heterocedasticidad. Para realizar este contraste es necesario llevar a cabo los siguientes pasos:

• a) Obtener los residuos del modelo estimado del modelo por mínimos cuadrados ordinarios ignorando la posible heterocedasticidad.
• b) Realizar una regresión de los residuos anteriores sobre una constante, las variables explicativas del modelo original, sus cuadrados y sus productos cruzados de segundo orden.
• c) Obtener el coeficiente de determinación (R²) de esta regresión y calcular el producto NR², donde N es el número de datos. Este producto sigue una distribución χ²_p-1, donde p es el número de variables explicativas utilizadas en el apartado b).

Ejemplo de contraste de White para los datos de consumo y renta trimestrales utilizados en los dos contrastes anteriores, donde en primer lugar se estima el modelo:

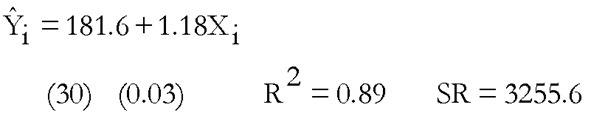
Se obtienen los residuos y se hace una regresión del cuadrado de los residuos sobre una constante, la renta y su cuadrado obteniendo:

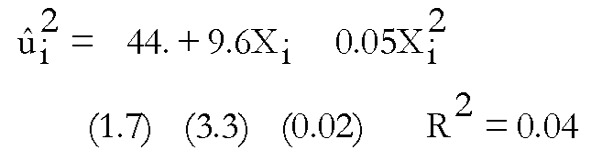
Así, NR²= 6.36 y el valor crítico de la χ²₂ 5.99, por lo tanto se rechaza la hipótesis nula de ausencia de heterocedasticidad.

Es importante destacar, que las conclusiones a las que se puede llegar al utilizar distintos contrastes de heterocedasticidad en un mismo modelo pueden ser diferentes, ya que cada uno de ellos plantea una hipótesis alternativa diferente.

Junto con los contrastes anteriores hay otro tipo de contrastes como pueden ser: el contraste de Glesjer, el contraste de Harvey, el contraste de Spearman, el de Koenker y Bassest, etc.

Heterocedasticidad condicional autorregresiva

Un aspecto importante en finanzas ha sido medir la respuesta de los agentes económicos respecto de la incertidumbre. Si para ello se utilizan datos de series temporales, en los que se supone que la varianza es constante, entonces la respuesta de los agentes no estará bien identificada. Es necesario utilizar la varianza condicional, mejor que la varianza no condicional, como una medida de la incertidumbre.

Así, los modelos de heteroscedasticidad condicional autorregresiva (modelos ARCH) han sido propuestos como una alternativa a los modelos ARIMA de series temporales, ya que al analizar los datos que proceden de este tipo de modelos, las perturbaciones son menos estables de lo que normalmente se supone. Por ello Engle (1982) propuso los modelos ARCH, para recoger los cambios que se producían en la varianza de una variable aleatoria y así obtener unas mejores predicciones, utilizando no solo la información disponible en el período presente, sino también la proporcionada por su pasado más reciente.

Un tipo de variable en la que la varianza condicional no se mantiene constante son, por ejemplo, los rendimientos financieros diarios. En este tipo de variables se observa un agrupamiento de la volatilidad, es decir, se produce una alternancia entre períodos de alta volatilidad seguidos de otros períodos en los que la volatilidad es menor. Un modelo de regresión adecuado para modelizar el comportamiento de este tipo de variables podría ser:

Y_t = X´_tβ + u_t

σ²_t = α₀ + α₁u²_t-1

donde u_t sigue una distribución Normal con media cero y varianza σ²_t. En este caso la varianza de las perturbaciones no se mantiene constante sino que cambia con los valores pasados del término de error.