Mapa de curvas de indiferencia

Concepto

Una curva de indiferencia es el lugar geométrico de las combinaciones de bienes (X,Y) que reportan al consumidor un mismo nivel de utilidad, es decir un cierto valor de la función de utilidad. Un mapa de curvas de indiferencia es un conjunto de curvas de nivel para una función de utilidad. Por ejemplo, partimos de una función Cobb Douglas, que es un tipo de función matemática que se emplea frecuentemente para expresar tanto funciones de utilidad como funciones de producción, ya que reúne las condiciones que se le exigen tanto a los mapas de curvas de indiferencia, de la teoría del consumo, como a los mapas de curvas isocuantas de la teoría de la producción (convexidad, decrecimiento, continuidad, etc.).

Una función de utilidad Cobb Douglas puede expresarse como:

U (x,y) = AX^αY^β

Por ejemplo, supongamos una función del tipo U = 100 X Y.

Buscamos ahora distintas combinaciones de puntos (X,Y) que permitan obtener un cierto nivel de utilidad y los vamos representando.

La ecuación a la que obedecen los puntos es la misma para todos, U = 100 X Y, lo que cambia es el nivel de U. Por ejemplo, buscaríamos pares X,Y para:

1.000 = 100 X Y

O para:

2.000 = 100 X Y

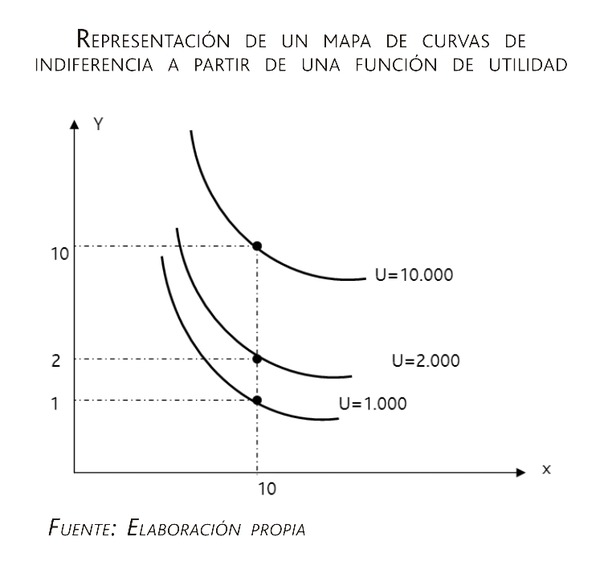
Si la función de utilidad cambia, entonces cambia el mapa, salvo que sea una transformación monótona creciente de aquella.

Propiedades de los mapas de curvas de indiferencia

Los mapas de curvas de indiferencia deben estar formados por curvas cuyo nivel de utilidad aumente a medida que estén situadas más lejos del origen, curvas estrictamente convexas, para que se refleje el hecho de que se valoran más los bienes escasos que los abundantes, curvas continuas, para cumplir el axioma de completitud y curvas que no se corten entre sí, para que se cumpla el axioma de transitividad.

Las curvas de indiferencia deben ser además decrecientes, para expresar el hecho de que la RMS entre X e Y (tasa subjetiva a la cual el individuo estaría dispuesto a cambiar 1 unidad de X por n unidades de Y) va cambiando, y para permanecer indiferente al individuo hay que ofrecerle menos cantidad de un bien a cambio de darle más del otro.

Puede suceder que alguna de estas propiedades no se cumplan (las curvas de indiferencia que las cumplen todas se llaman neoclásicas) y esto da lugar a soluciones de esquina en el equilibrio del consumidor.

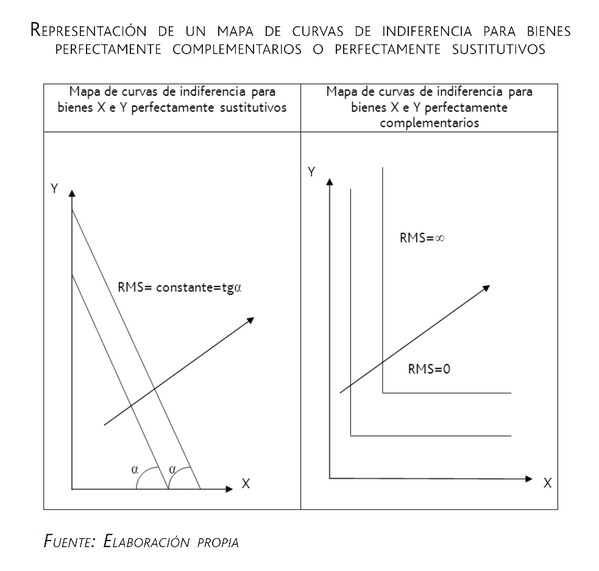
Por ejemplo, son anómalos los mapas de curvas de indiferencia cuando los dos bienes son perfectamente complementarios o bien cuando los dos bienes son perfectamente sustitutivos en el consumo.

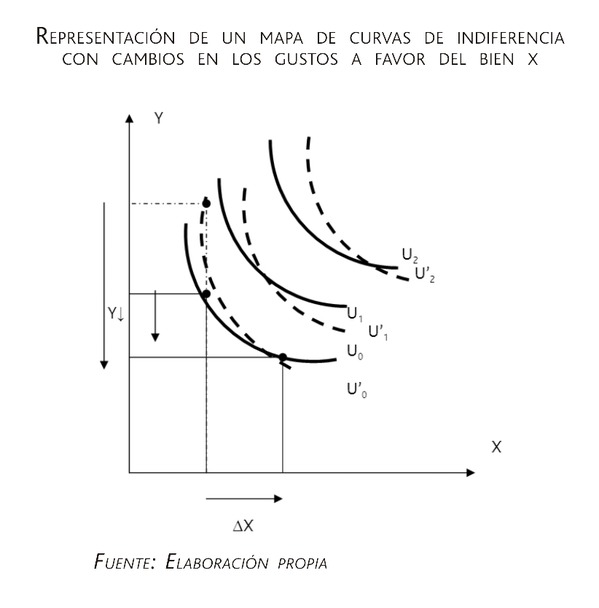
Cambios en los mapas de curvas de indiferencia

Cada consumidor tiene unas preferencias respecto a los bienes X e Y expresadas por su propio mapa, por lo que los mapas de los individuos no tienen por qué coincidir. Si los gustos de un consumidor cambian, por ejemplo por una campaña de publicidad a favor del bien X y en contra del bien Y, su RMS entre los bienes X e Y debe aumentar en cada punto y su nuevo mapa se vería alterado.