Modelo de valoración de opciones en Black y Scholes

Concepto

La propuesta de Black y Scholes en 1973, fue la primera solución explícita para obtener el precio de una opción sencilla y dio lugar a la moderna teoría de valoración de opciones.

Hipótesis

Para obtener la fórmula de valoración de una opción en función del precio de la acción, Black y Scholes, y al igual que el método binomial, suponen una serie de "condiciones ideales" o hipótesis de partida del mercado, tanto para la acción como para la opción. Estas hipótesis básicas son las siguientes:

• 1. Se suponen mercados de capitales competitivos y perfectos, en los que no hay impuestos, costes de transacción o limitaciones a la operatoria en descubierto.
• 2. No existen restricciones sobre compras o ventas a corto plazo de títulos y opciones, por lo que el volumen de transacciones no afectará al precio de mercado de los títulos.
• 3. Existe una tasa de interés sin riesgo, rf, conocida y constante a lo largo del tiempo. Es posible prestar y pedir prestado cualquier cantidad de dinero al tipo de interés sin riesgo.
• 4. La negociación en los mercados es continua.
• 5. La acción o título básico no paga dividendos ni otro tipo de distribución de beneficios, reservas o capital.
• 6. El precio de la opción call solo depende del precio del título básico, del tiempo y de variables que se suponen constantes conocidas.
• 7. La tasa de retorno instantánea sobre el precio del título sigue un proceso de difusión con media constante, a, y varianza σ2 instantánea constante (proceso de Wiener).

Fórmula Black-Scholes de valoración del precio de una opción de compra europea:

C = S · N(d₁) - E · e^-r,t · N(d₂)

siendo:

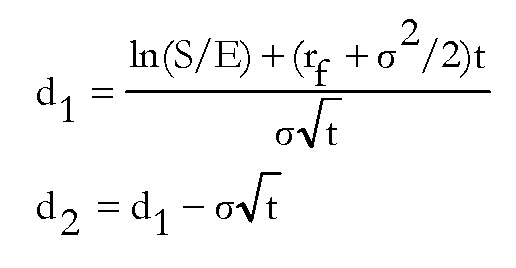
donde:

c = prima de la opción de compra.

S = precio actual de la acción.

E = precio de ejercicio de la opción.

r_f = tasa de interés sin riesgo.

t = tiempo que falta para la expiración de la opción.

σ² = varianza instantánea del rendimiento de la acción.

N(d) = función de distribución normal.

Para el caso de una opción de venta:

P = E · e^-r,t · N(d₂) - S · N(d₁)

Siendo p la prima de la opción de venta.

El modelo de valoración de opciones de Black y Scholes presenta gran simplicidad, puesto que una vez calculados d₁ y d₂, para obtener N(d) solo hay que consultar las tablas estandarizadas de la distribución normal.

Posteriormente, Black-Scholes desarrollaron en 1976 una fórmula para valoración de opciones sobre contratos de futuros partiendo de las siguientes hipótesis:

• 1. La distribución de precios del contrato de futuros sigue una lognormal.
• 2. Las cotizaciones de los contratos varían de forma continua, sin saltos.
• 3. Existe una tasa de interés sin riesgo, r_f, conocida y constante a lo largo del tiempo. Es posible prestar y pedir prestado cualquier cantidad de dinero al tipo de interés sin riesgo.
• 4. La desviación estándar del rendimiento del contrato (volatilidad) es constante.
• 5. No existen costes de transacción ni impuestos.
• 6. No existen restricciones para comprar o vender en descubierto ni de forma fraccionada.

La fórmula resultante es la siguiente:

Fórmula Black-76 para opciones CALL europeas sobre futuros:

C = e^-rt(F · N(d₁) - E · N(d₂))

donde:

F = precio del futuro.

E = precio de ejercicio de la opción.

t = tiempo que falta para la expiración de la opción.

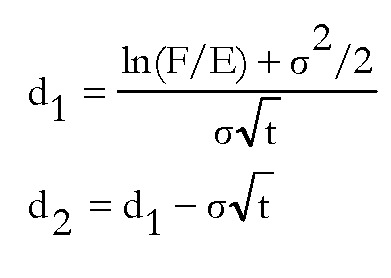
σ = volatilidad del futuro.

N(d) = función de distribución normal.

En el caso de una opción PUT:

P = (E - F)e^-rt + c