Concepto
Los modelos de variable dependiente truncada y censurada se refieren a modelos econométricos donde la variable dependiente solo representa a una parte de la población, por ejemplo, aquellos cuya renta sea superior a un determinado umbral. Esto significa que solo tenemos disponibles datos para una subpoblación inferior a la población total y que, por lo tanto, habrá que diseñar métodos estadísticos específicos en el análisis de regresión habitual para tener en cuenta las modificaciones inducidas en la distribución estadística de la variable dependiente truncada o censurada (por ejemplo: la media de la variable truncada o censurada no será la misma que la original).
Introducción
Una distribución truncada es una distribución en la que los valores por debajo (o por encima) de un determinado umbral no se pueden observar, por lo tanto, la función de densidad de la variable truncada vendrá dada por:

donde f(x) representa la función de densidad de la variable original, a es el punto de truncamiento original y F(a) es la función de distribución de la variable original en el punto a (mide la probabilidad acumulada hasta ese punto). Como consecuencia, si se conoce la distribución de la variable original, también se puede conocer la distribución de la variable truncada; a modo de ejemplo el gráfico inferior reproduce una distribución original normal de media 1 y desviación típica 3 junto con la distribución truncada a partir del punto a=0.
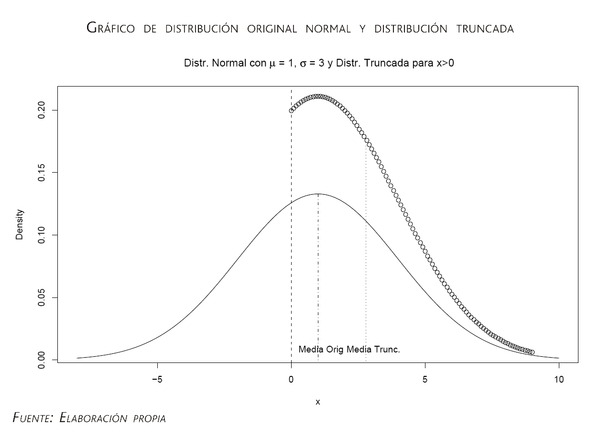
A partir del gráfico es inmediato apreciar que, aunque la forma de la distribución truncada es similar a la de la distribución original, el área por debajo de la función de densidad ha tenido que cambiar para que siga sumando uno. Como consecuencia, las características de la distribución cambian, por ejemplo la media de la distribución truncada (cuyo valor es 2.795) se desplaza a la derecha respecto a la original (que valía 1) debido al truncamiento en a=0. Por el contrario la desviación típica de la distribución truncada (1.995) es menor que la desviación típica de la distribución original (3), ya que el truncamiento conlleva una menor dispersión de la distribución. Al igual que a partir de la distribución original, si se conoce el punto de truncamiento, se pueden inferir las características de la distribución truncada, también es posible realizar el proceso inverso; es decir, a partir de la distribución truncada intentar conocer características de la distribución original. A modo de ejemplo, una encuesta realizada en USA para el 2 % de los hogares que tenían ingresos mayores de 100.000$ mostraba que la media de estos hogares era de 142.000$. A partir de estos datos, realizando una hipótesis de distribución logarítmico-normal para la renta (lo cual querría decir que el logaritmo de la renta tiene una distribución normal), se puede inferir que la media de la renta en la población global sería de 22.087$ (en ese año de 1987 la media publicada fue de unos 25.000$). Con solo conocer datos sobre una parte pequeña de la población (en este caso los más ricos) se pueden inferir características sobre toda la población.
La distribución censurada de una variable se refiere a la misma idea de la distribución truncada pero, en lugar de no disponer de datos a partir de un cierto valor, se asigna a toda la distribución por debajo (o por encima) de un umbral el valor de ese umbral. Por ejemplo, una distribución censurada desde el cero quiere decir que asignaríamos el valor cero a toda la distribución de la variable por debajo de esa cantidad. Un ejemplo económico de censura de una variable puede ser la asistencia a un campo de fútbol: si el aforo del campo es de 40.000 espectadores, cada vez que se llena solo podemos observar el valor 40.000 aunque la demanda real fuera superior a ese valor. Técnicamente, la distribución de la variable censurada es una mezcla entre la distribución original hasta el punto de censura y el resto de la distribución se acumula en el umbral de censura, es decir, la demanda censurada sería la original hasta el valor 40.000 y toda la probabilidad desde el 40.000 hacia la derecha se acumularía en ese punto.
Modelos de regresión con variable dependiente truncada o censurada
En econometría es frecuente que se planteen modelos de regresión donde una variable dependiente "y" venga explicada por un vector de variables independientes x en la forma:
y = xTβ + u u∼N(0,σ)
donde los coeficientes β de regresión representan los efectos de cada variable independiente xi sobre la variable dependiente y. La variable u es el término de perturbación aleatorio de la regresión y recoge todos los efectos que influyen sobre la variable y que no están recogidos en el vector x. Una forma de interpretar esta regresión es diciendo que la media condicionada de la variable y, dadas las variables independientes x, viene dada por E[y/x]= xTβ y que la perturbación u representa las desviaciones de y respecto a su media condicional, las cuales tienen una distribución aleatoria normal de media cero y varianza constante. Como el interés de la regresión, habitualmente se centra en la estimación de los parámetros β (los cuales miden los efectos marginales de las x sobre la y), con las hipótesis del modelo anterior se pueden estimar fácilmente estos parámetros utilizando el estimador lineal por mínimos cuadrados ordinarios (o MCO).
Si la variable dependiente estuviera truncada por la izquierda a partir de un punto a, y la distribución de la perturbación en el modelo original fuera normal, como hemos supuesto anteriormente, se puede demostrar que la media condicional de y ya no sería la del modelo anterior sino que vendría dada por la expresión:
y = xTβ + σλ + u
σ = ø[(a- xTβ)/σ]/{1-Ф[(a- xTβ)/σ]}
donde las funciones ø y Ф representan las funciones de densidad y de distribución de la normal estándar, respectivamente. Lo importante es observar que, a diferencia del caso anterior, los parámetros β ya no representan directamente la influencia de las variables independientes x sobre la variable dependiente y. Además, el modelo es no lineal en β y la estimación de estos parámetros no se puede realizar por el método sencillo MCO, como en el caso previo, sino que hay que utilizar técnicas de máxima verosimilitud junto con algoritmos numéricos de optimización. Afortunadamente, gran parte del software especializado incluye opciones para estimar este tipo de modelos de forma rutinaria. Una vez estimado el modelo, las dependencias de la variable y respecto a las x se pueden obtener a partir de los efectos marginales, dados por:
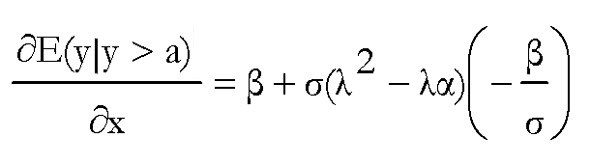
donde λ es la misma expresión que anteriormente y α=[(a - xTβ)/σ]. Lo importante es observar que, aunque las influencias de las variables independientes no vienen dadas directamente por β, una vez estimado el modelo estos efectos marginales pueden calcularse fácilmente. Dichos efectos miden el cambio en la media de la variable dependiente truncada, cuando la correspondiente variable independiente x cambia de forma marginal.
Si los datos estuvieran censurados en lugar de truncados, la media condicionada de la variable y, dados los valores de las x, también cambiaría respecto a la regresión normal. En este caso la forma que tendría la regresión sería la siguiente:
y =Ф(xTβ/σ)( xTβ+σλ) + u
donde el valor de λ es el mismo que anteriormente. Este es el modelo Tobit o modelo de regresión censurada, el cual, debido a que no es lineal en β, tampoco puede estimarse por MCO y hay que utilizar técnicas de máxima verosimilitud. Los efectos marginales (cambio en la media de la variable y al cambiar marginalmente la x) vienen dados por:
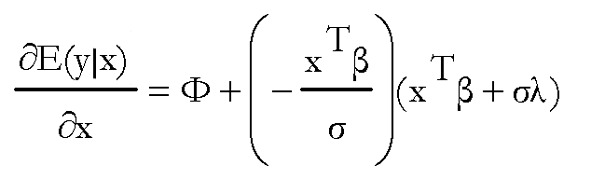
De nuevo, una vez estimados los parámetros del modelo, es fácil calcular estos efectos marginales.
Cuando se estima un modelo Tobit hay que tener en cuenta que las estimaciones son muy sensibles a los problemas de especificación que pudieran darse en el modelo. Por ejemplo, si las perturbaciones u son heterocedásticas (la varianza de las perturbaciones cambia para cada observación) o su distribución no fuera normal, las estimaciones obtenidas no serían consistentes, a diferencia de lo que ocurre con el modelo de regresión habitual. Esto hace que la fase de diagnosis del modelo estimado sea especialmente relevante en estos modelos y un análisis de residuos, así como la realización de contrastes de especificación, es muy importante para poder validar el modelo estimado.
Hay que señalar que se han desarrollado bastantes extensiones de los modelos de truncamiento y variable dependiente censurada a partir de los expuestos anteriormente. Uno de los casos más utilizados ha sido el modelo de regresión con selección muestral. En este caso se establece un problema con dos fases, una primera ecuación modeliza si se da o no el fenómeno y otra ecuación cuantifica ese fenómeno para aquellos individuos en los que se observa. Un ejemplo puede ser la modelización de la oferta de empleo con una primera ecuación de participación en el mercado de trabajo que modeliza la diferencia entre el salario de mercado y el salario de reserva de una persona como función de características individuales (edad, nivel educativo,...). Posteriormente, una segunda ecuación de resultados puede modelizar el número de horas de trabajo ofertadas en función de características del hogar (número de hijos,...). Hay que tener en cuenta que esta segunda ecuación solo tiene valores observados para aquellos individuos cuyo salario de mercado está por encima del salario de reserva y, por lo tanto, la variable número de horas muestra un truncamiento selectivo.
Recuerde que...
- • En los modelos de variable dependiente truncada y censurada significa solo tenemos disponibles datos para una subpoblación inferior a la población total, por lo que habrá que diseñar métodos estadísticos específicos en el análisis de regresión habitual para tener en cuenta las modificaciones inducidas en la distribución estadística de la variable dependiente truncada o censurada
- • La distribución censurada de una variable se refiere a la misma idea de la distribución truncada pero, en lugar de no disponer de datos a partir de un cierto valor, se asigna a toda la distribución por debajo (o por encima) de un umbral el valor de ese umbral.
- • Uno de los casos más utilizados ha sido el modelo de regresión con selección muestral. En este caso se establece un problema con dos fases, una primera ecuación modeliza si se da o no el fenómeno y otra ecuación cuantifica ese fenómeno para aquellos individuos en los que se observa.
- • Cuando se estima un modelo Tobit hay que tener en cuenta que las estimaciones son muy sensibles a los problemas de especificación que pudieran darse en el modelo.