Concepto
Es una medida de la sensibilidad de la rentabilidad de un activo financiero ante cambios en la rentabilidad de una cartera de referencia o comparación. Por tanto, la beta nos indica cómo variará la rentabilidad del activo financiero si lo comparamos con la evolución de una cartera o índice de referencia. Habitualmente, la cartera o índice de referencia corresponderá al índice bursátil más representativo donde se negocia el activo financiero. Así por ejemplo, para acciones negociadas en la Bolsa española se suele tomar como índice de referencia el IBEX-35 y para acciones cotizadas en la Bolsa de Nueva York se puede utilizar el S&P 500.
Rango de valores
Los valores que puede tomar la beta de un activo financiero pueden ser muy variados. De hecho, su rango de posibles valores no está acotado. No obstante, existen unos niveles típicos de beta de un activo financiero y que podemos agrupar en los siguientes:
- — Beta igual a uno: en este caso, la rentabilidad del activo financiero se va a comportar igual que el índice de referencia. Si por ejemplo, el índice de referencia fuese el S&P 500, y este sube un 7 % entonces el activo financiero en cuestión también debería ascender un 7 %. Pero, cuidado, porque la réplica del movimiento también se produciría en el caso de que el índice cayera, y por tanto, el activo financiero debería bajar en la misma proporción que lo hiciera el índice.
- — Beta mayor que uno: en esta situación, el activo financiero va a mostrar una mayor variabilidad que el índice de referencia y, por tanto, amplificará los movimientos del mercado, tanto al alza como a la baja. Por ejemplo, para una beta igual a 1,5, si el índice bajara un 5 %, el activo descenderá un 7,5 %.
- — Beta menor que uno: en este caso, el activo financiero en cuestión es de corte defensivo y presenta una menor variabilidad que el índice de referencia. Para el mismo ejemplo que el caso anterior, pero con una beta de 0,5, el activo financiero solo caería la mitad, esto es, un 2,5 %.
Como la beta es un dato relativo, también se puede interpretar en forma de porcentaje. Por ejemplo, una beta de 1,30 significa que el activo financiero es un 30 % (1,30 - 1,10) más variable que el índice. Y para una beta de 0,80, esta indica que el título en cuestión es un 20 % (0,80 - 1,00) menos volátil que el índice.
La siguiente tabla recoge las betas para algunos de los valores cotizados en la bolsa española. Las distintas columnas se refieren a datos obtenidos de las últimas 20, 60, 120 y 250 sesiones bursátiles.
BETAS DE EMPRESAS ESPAÑOLAS COTIZADAS| Empresa | 20 | 60 | 120 | 250 |
| ACS | 0,71 | 0,71 | 0,77 | 0,77 |
| BBVA | 1,82 | 1,84 | 1,55 | 1,35 |
| DOGI | 0,47 | 0,67 | 0,47 | 0,65 |
| GAMESA | 1,54 | 1,57 | 1,67 | 1,46 |
| IBERDROLA | 0,77 | 1,06 | 1,17 | 1,20 |
| INDRA | 0,57 | 0,42 | 0,49 | 0,50 |
| INDITEX | 0,98 | 0,87 | 0,85 | 0,79 |
| MAPFRE | 1,29 | 1,24 | 1,07 | 0,96 |
| NH HOTELES | 0,91 | 1,13 | 0,80 | 0,77 |
| RED ELÉCTRICA ESPAÑOLA | 0,31 | 0,36 | 0,42 | 0,55 |
| TELEFÓNICA | 0,41 | 0,51 | 0,60 | 0,77 |
| Fuente: Informe mensual Sociedad de Bolsas, abril de 2009 |
Como podemos comprobar en la anterior tabla, los valores de las betas varían sensiblemente de una empresa a otra debido, esencialmente, al distinto nivel de riesgo económico (procedente de la actividad económica principal de la empresa en cuestión) y también al diferente riesgo financiero de las mismas, (afectado por la estructura financiera empresarial). Tomando como referencia la columna de datos para las últimas 250 sesiones bursátiles, hay tres títulos que se pueden considerar como agresivos (betas mayor que uno), uno que se puede considerar como neutro (Mapfre con una beta próxima la unidad) y los siete restantes que se catalogarían como títulos defensivos (betas menor que uno).
Por otro lado, los valores de las betas también quedan condicionados por el período temporal que se fije para su cálculo. En función del horizonte temporal de la inversión, se puede fijar como referencia uno de ellos.
Por último, es bastante improbable que la beta de un activo financiero tome valores negativos y, por tanto, muestre un comportamiento inverso al del mercado en el que se negocian. Esta situación se asimilaría a la contratación de una especie de seguro, ante posibles movimientos adversos del mercado. En la realidad, pueden existir este tipo de activos “refugio” como así ha ocurrido y sigue sucediendo con la inversión en determinados metales preciosos como el oro; si bien se ha de tener en cuenta que no se trata de activos financieros. Estas inversiones muestran su carácter “refugio” en toda su plenitud, sobre todo en las épocas de crisis financieras.
Clasificación y valores objetivo
Como se ha comentado previamente, la beta de un activo financiero expresa la sensibilidad del rendimiento de un título respecto a las variaciones del mercado. De esta manera, dependiendo de la dirección que tome el mercado, el dato de beta puede constituir en sí mismo algo positivo o negativo. En base al anterior razonamiento se puede distinguir entre:
- 1. Betas alcistas: miden el comportamiento que ha tenido un valor respecto al mercado en épocas de subidas.
- 2. Betas bajistas: en este caso el análisis de sensibilidad se centra en períodos de descensos del mercado.
Con la información proporcionada por estas betas, podemos identificar el comportamiento de nuestro título dependiendo de si el mercado es alcista o si, en cambio, es bajista. Obviamente, los valores objetivo de las betas alcistas y de las betas bajistas serán, en la medida de lo posible, mayores que uno, para el caso de las primeras, (así se amplía el movimiento del mercado alcista) y menores que uno, para las segundas, (así se minora el movimiento del mercado bajista).
Cálculo
Matemáticamente, la beta de un activo financiero podemos calcularla como el cociente entre la covarianza de la rentabilidad del activo financiero y la cartera de referencia, y la varianza de la rentabilidad de esta última cartera. Esto es,
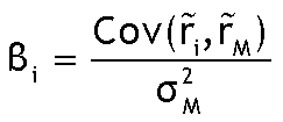
La anterior expresión matemática proviene de una técnica estadística conocida como análisis de regresión, y no es más que la estimación por mínimos cuadrados ordinarios del parámetro beta de la recta de regresión. Veamos un sencillo ejemplo que nos lo muestre. El siguiente gráfico recoge 60 observaciones de rentabilidades mensuales a lo largo del período 2003-2008 de la empresa General Electric y el índice S&P 500.
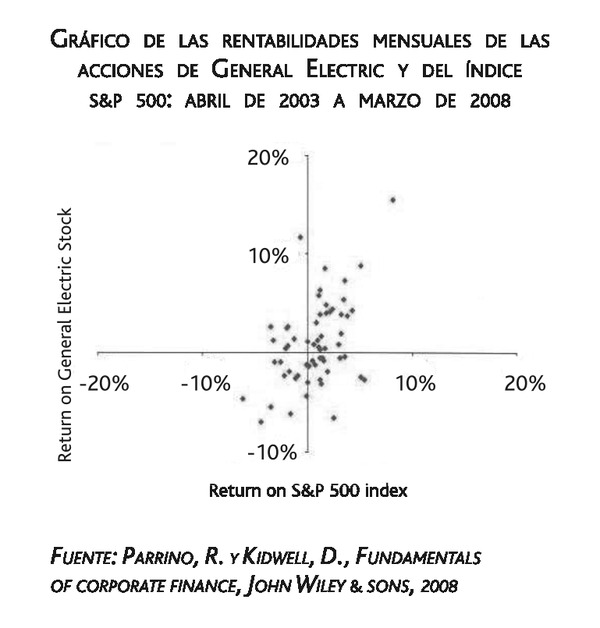
En el gráfico podemos observar que la rentabilidad de las acciones de General Electric tiende a ser elevada cuando la rentabilidad del S&P 500 también lo es. La beta no es otra cosa que una medida estadística de esta relación. Así, podemos cuantificar la relación entre la rentabilidad de las acciones de General Electric y el mercado bursátil norteamericano, calculando la pendiente de la línea recta que mejor se ajusta a la nube de puntos reflejada en la figura.
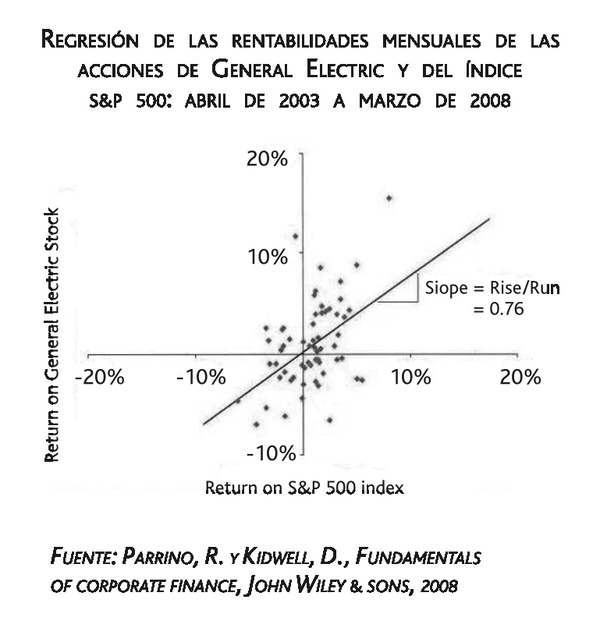
Nótese que la pendiente de la recta de regresión es 0,76. Este valor implica que, en promedio, la variación de la rentabilidad de las acciones de General Electric fue 0,76 veces la variación de la rentabilidad del S&P 500. Por tanto, si el índice S&P 500 aumenta un 1 %, el incremento promedio de las acciones de General Electric es de un 0,76 %. Esta es una medida de riesgo sistemático (véase “Riesgo sistemático”) porque nos indica que la volatilidad de los rendimientos de las acciones de General Electric supone 0,76 veces la del S&P 500 en su conjunto.
Por último, recordar que la beta de un determinado activo financiero está basada en su comportamiento histórico, por lo que proporciona solo una estimación de cuál puede ser su beta en el futuro.
Recuerde que...
- • La beta nos indica cómo variará la rentabilidad del activo financiero si lo comparamos con la evolución de una cartera o índice de referencia.
- • Los valores que puede tomar la beta de un activo financiero pueden ser muy variados. De hecho, su rango de posibles valores no está acotado.
- • Como la beta es un dato relativo, también se puede interpretar en forma de porcentaje.
- • La beta de un activo financiero podemos calcularla como el cociente entre la covarianza de la rentabilidad del activo financiero y la cartera de referencia, y la varianza de la rentabilidad de esta última cartera.